Aplikace STAT 1
Neubauer, J. Sedlačík, M. a Kříž O. Základy statistiky: Aplikace v technických a ekonomických oborech. Praha: Grada, 2012. ISBN 978-80-247-4273-1.
Testy statistických hypotéz
Jednovýběrové testy
Aplikace STAT1 obsahuje tyto jednovýběrové testy hypotéz: test střední hodnoty a rozptylu normálního rozdělení (list "1V - normální"), test střední hodnoty pro velké výběry (list "1V - libovolné") a test parametru alternativního rozdělení pro velké výběry (list 1V a 2V - podíly). Testování se ve všech případech provádí podobně, zaměříme se na jeden konkrétní - test střední hodnoty normálního rozdělení. Přejdeme na list "1V - normální" a vybereme datový soubor. Zvolíme hladinu významnosti α (implicitně nastaveno na hodnotu 0,05), zadáme nulovou hypotézu H a vybereme jednu ze tří nabízených alternativních hypotéz A.
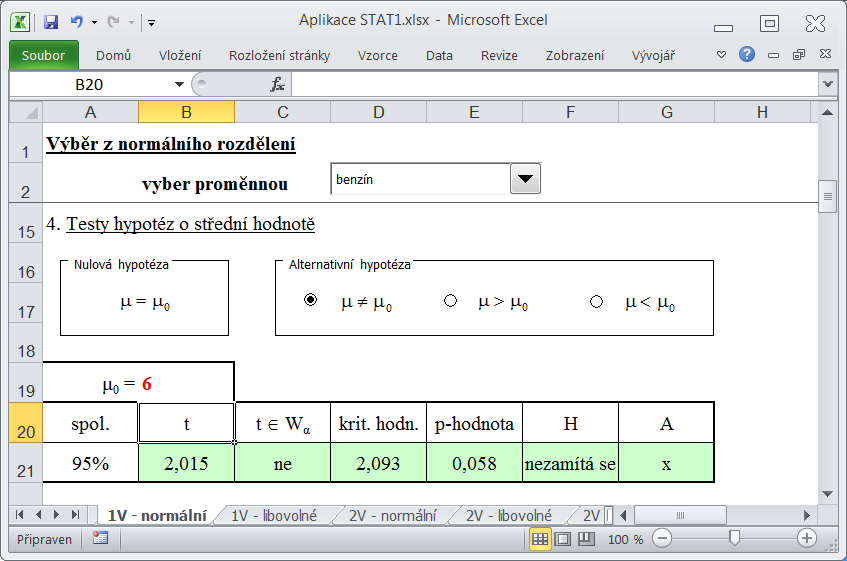
Jako výstup obdržíme hodnotu testového kritéria, kritickou hodnotu, p-hodnotu a slovní odpověď (H se nezamítá, nebo H se zamítá A se přijímá). Testy je možné také počítat zadáním číselných charakteristik (v dolní části listu).
Dvouvýběrové testy
Aplikace STAT1 obsahuje tyto dvouvýběrové testy hypotéz: test shody dvou rozptylů nezávislých normálních rozdělení (list "2V - normální"), test shody dvou středních hodnot nezávislých normálních rozdělení (za předpokladu homoskedasticity a heteroskedasticity - list "2V - normální"), test shody dvou středních hodnot pro velké nezávislé výběry (list "2V - libovolné"), test shody dvou středních hodnot pro závislé výběry (párový test - list "2V - párový test") a test shody dvou parametrů alternativního rozdělení pro velké nezávislé výběry (list 1V a 2V - podíly). Testování se provádí podobně jako u jednovýběrových testů, zde je třeba vybrat dva datové soubory.
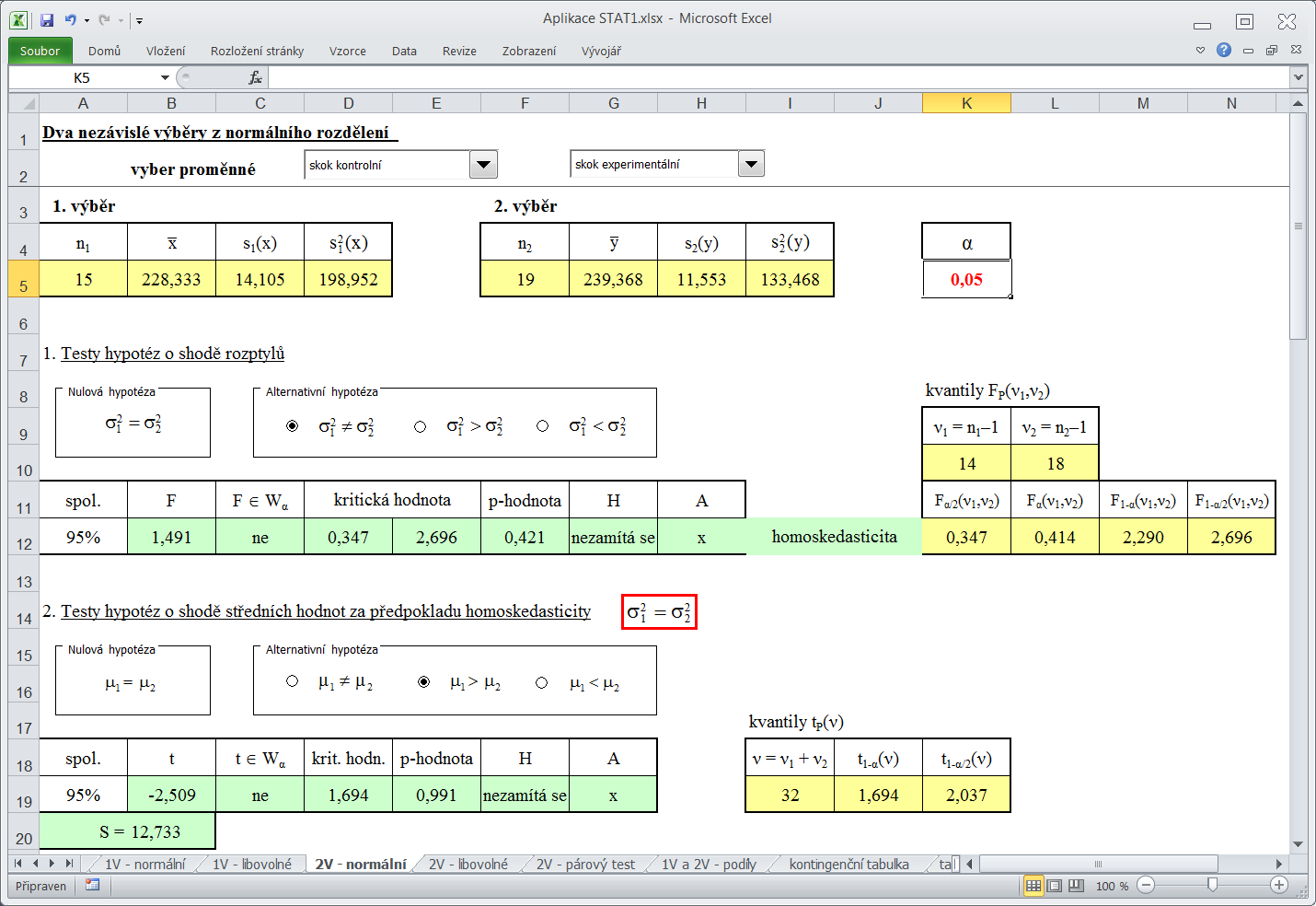
Testy normality
Základní představu o tvaru rozdělení datového souboru můžeme získat konstrukcí histogramu, případně polygonu četností (viz intervalové a bodové rozdělení četností). V listu "popisné charakteristiky" lze nalést kromě krabicového diagramu i Q-Q plot porovnávající teoretické kvantily normovaného rozdělení N(0,1) s empirickými kvantily určených z dat. Leží-li tyto body přibližně na přímce, můžeme usoudit, že zkoumaný náhodný výběr pochází z normálního rozdělení.
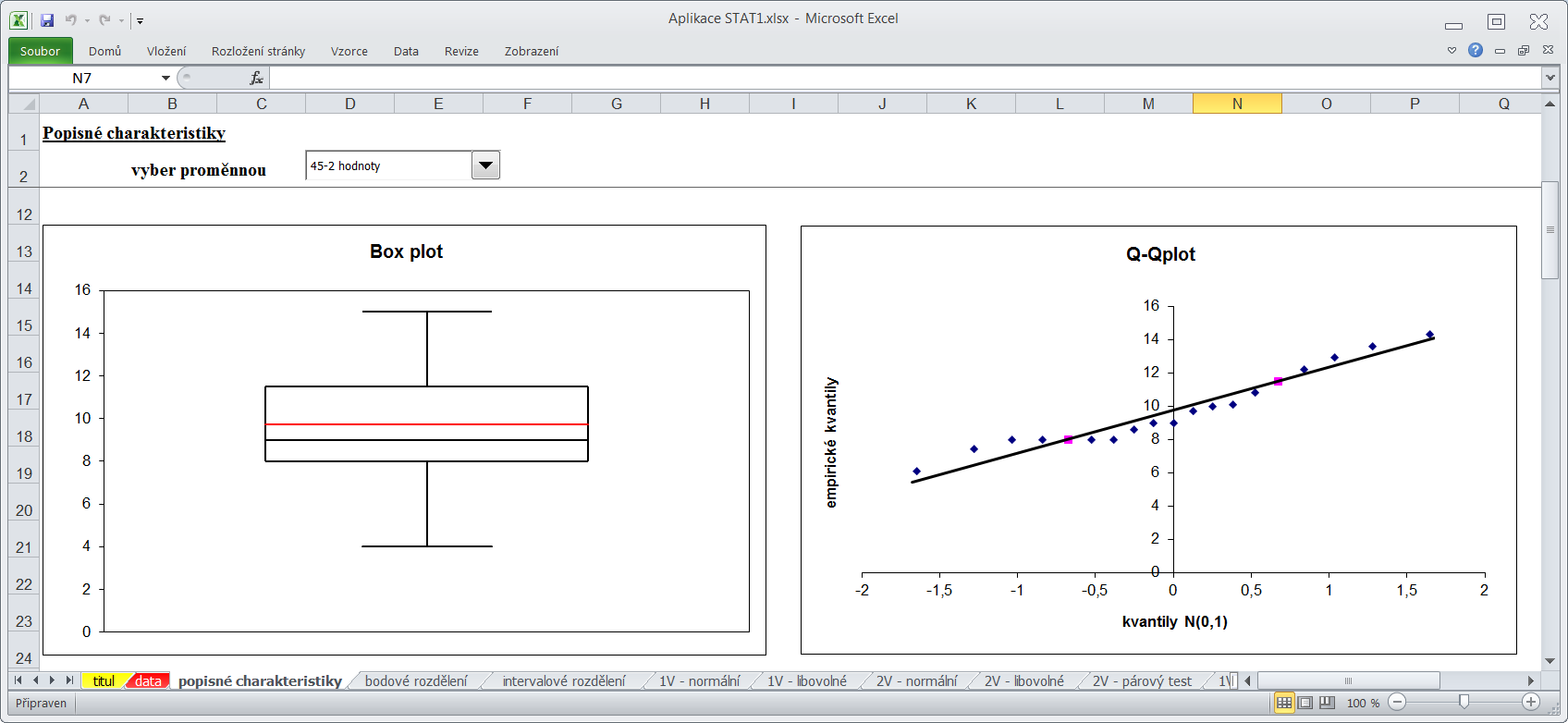
Listy "popisné charakteristiky", "bodové rozdělení" a "intervalové rozdělení" obsahují v dolní části testy normality založené na výběrových koeficientech šikmosti a špičatosti.
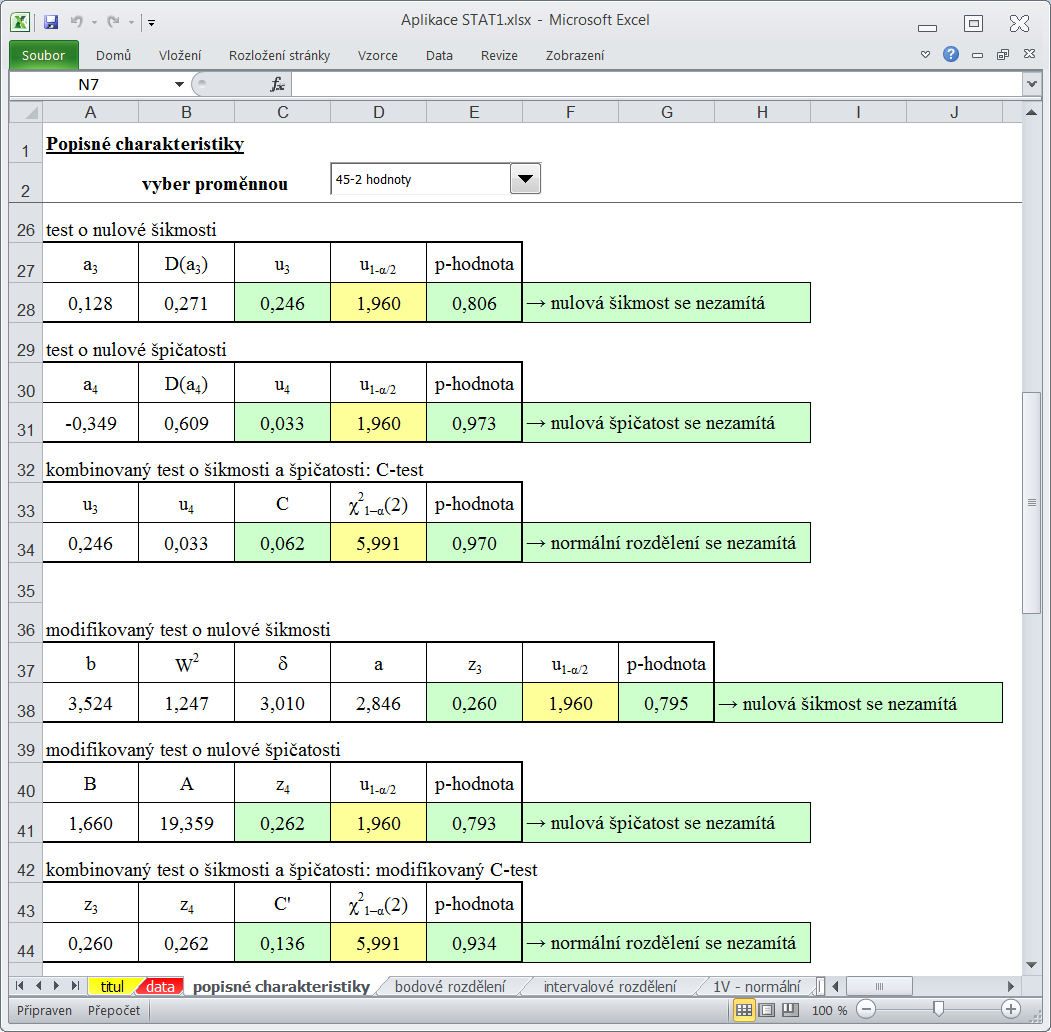
Výpočet těchto testů zadáním potřebných charakteristik (rozsah, koeficient šikmosti a špičatosti) lze provést v dolní části listu "popisné charakteristiky".